第三章：恒星大气模型和恒星连续光谱

1. 非灰大气辐射平衡理论的一般解法

吸收系数随频率或波长变化的大气被称为非灰大气。

吸收系数对非灰连续谱的影响

假设真实的源函数近似有线性的温度分布(忽略泰勒展开的高阶向) 代入恒星表面的辐射强度得恒星表面的辐射流这就是爱丁顿-巴比叶关系。上式表明，恒星表面的辐射流等于光深处的源函数。

而非灰大气下，由于吸收系数是频率的函数，不同波长对应的几何深度就不再相同。

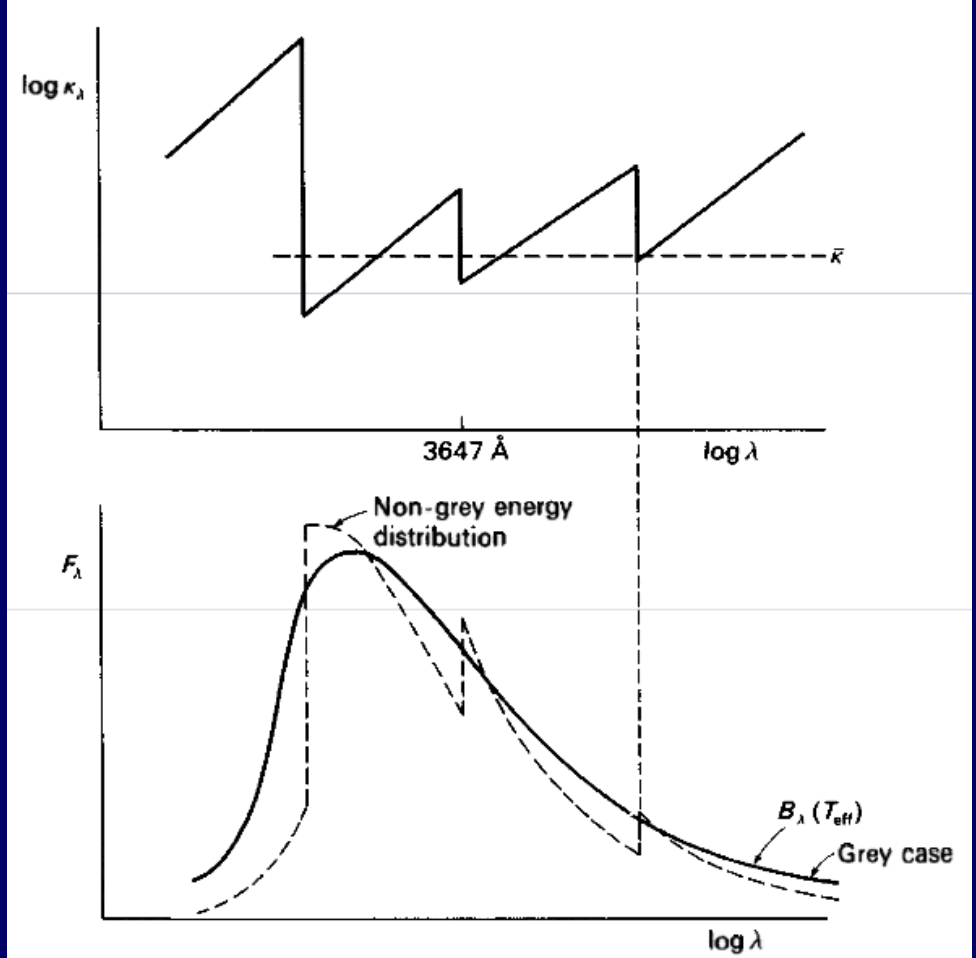
图示表明，辐射流看起来是吸收系数随波长分布的镜像。在不连续的波长处也对应辐射流的跳变。

巴尔末跳跃对UBV颜色的影响

色指数

颜色指数定义为两个波段的视星等之差，可以反映天体的温度。

B波段：445nm；V波段：550nm；U波段：365nm

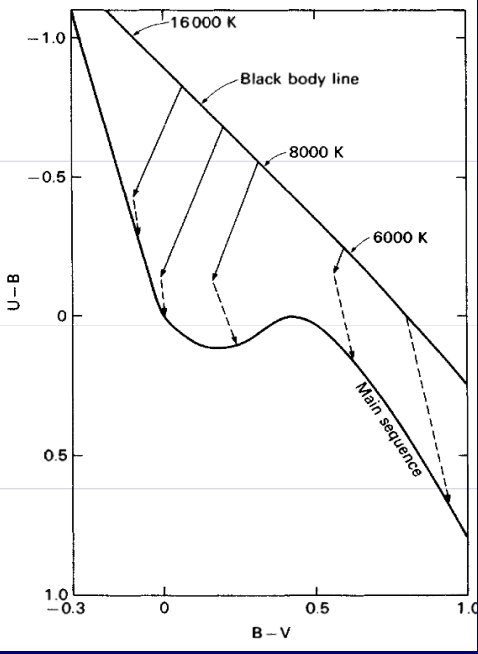
对于黑体，B-V与U-B在温度较高时都与温度线性相关，所以得到的双色指数图是一条直线

对于灰大气，可以认为观测到的辐射都来自于的相同大气深度，所以是此处温度的黑体谱

对于黑体谱的偏离

在巴尔末跳跃长波一侧吸收系数较小，观测接受到更多的辐射。所以在蓝端（B波段）会观测到比灰大气更多的辐射；在波长更长的可见光光谱区（V波段）情况相反。综合起来造成B-V变小，即为图中实线箭头所示。

除此之外，吸收系数还会因为谱线的线吸收变化，导致色指数更红，即为图中虚线箭头所示。

非灰大气的温度分布

一般采用逐次近似的方法，用灰大气作为第一级近似。引用某种加权的平均吸收系数

罗斯兰平均

定义平均吸收系数给出灰大气中一样的辐射流.

用乘以辐射转移方程并积分，并引入爱丁顿参量

对恒星大气深层，认为辐射场各向同性：用乘以辐射转移方程并积分

所以：代入的表达式代入导数关系式

对于灰大气，总辐射流：

定义平均吸收系数得：即为罗斯兰权重系数，为罗斯兰平均吸收系数。 ##### 钱德拉塞卡平均，普朗克平均

非灰大气辐射平衡的解法

确定后，可以构造一个等价的灰大气：温度随深度的变化由灰大气钱德拉塞卡解给出：在爱丁顿近似中.

真实大气的光学深度根据与，与（将在下一节中获得）的关系，可以将表示为的已知函数，就可以代入辐射转移方程的形式解，得出，即为第一级近似的结果。

2. 计算恒星大气模型的一般方法

流体静力学平衡方程

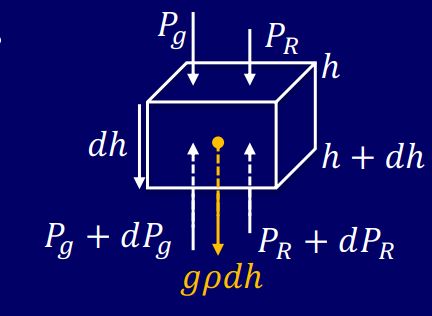图中表示气体作用产生的压强，表示辐射作用产生的压强。由图可知流体静力学平衡方程为：用光学深度表达：对于

利用灰大气中的关系得代入流体静力学平衡方程： #### 气体压力与重力加速度的依赖关系一般来说是和的函数，对于确定的大气，和都是的函数，所以可以将写为的函数。

这个函数可以用一个简单的多项式来近似代入流体静力学平衡方程

积分并取边界条件时，

3. 早型光谱型恒星的大气模型和连续光谱能量分布

A型星的大气吸收中氢元素占着主导作用，考虑的吸收是的已知函数，取罗斯兰平均即可得到平均吸收系数

通过萨哈公式可以得到的关系：

其中是对电离度求和，是对元素种类求和。而每种元素的相对含量已知，可以化为的已知函数。

另一方面，由的计算公式可以得到通过消去即可得到此关系。从而通过数值积分即可得到。

4. 对流

倘若辐射平衡是不稳定的，则任何轻微的扰动都会导致大规模的质量运动和能量以对流方式的转移。当流体或气体中存在很大的温度梯度时，会容易出现对流运动。

史瓦西稳定判据

在恒星大气中任取一小体元，设扰动使它上升dr，假设扰动局促使得没有能量交换，那么它会绝热膨胀。设原始位置体元的物理量：其中带表示体元的物理量，不带表示环境物理量。

扰动后所以当时，体元会回落，整个体系是稳定的；反之体元继续上升，形成对流。

利用泰勒展开保留到一阶稳定条件化为 $绝热$ 若平均原子量是常数，由理想气体方程利用绝热过程，代入稳定条件消去 $绝热大气$ 另一种常用的形式为： $绝热大气$ 若不是常数，对流条件变为

对流不平衡的原因

辐射平衡温度梯度

由罗斯兰平均系数计算中得到的的计算公式再在流体静力学平衡方程中忽略辐射压所以 1. 很大时会让变得很大，这一般发生在恒星中心：所有光度都产生在很小的空间时

随深度急剧增大时。由流体静力学平衡方程以及的近似：上式表明其实不依赖的绝对值，只有b较大才比较明显

绝热温度梯度

对于单原子气体所以对于多原子分子气体，若自由度为所以大量分子存在的大气对流极易产生。

此外当大气从电离氢过渡到中性氢时，将增大一倍，也将加强对流的产生。

由氢电离产生的对流区称为氢对流区；氦电离产生的为氦对流区。大多数恒星这两个对流区融合在一起形成一个对流区。