第二章：恒星大气的连续不透明度

原子的激发和电离

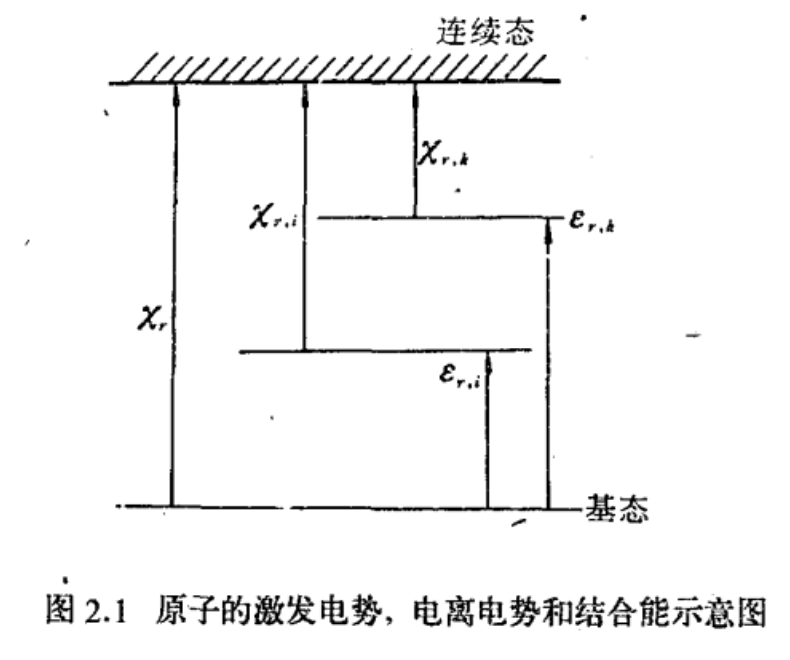
电离电势：一个处于基态的原子电离所需的最小能量称为原子的电离电势。通常用表示次电离的原子再电离时的电离电势。用表示次电离原子的能级的激发电势
结合能：把原子从某一个激发能级电离所需的最小能量称为这个能级的结合能，用表示，则有：

玻尔兹曼公式

玻尔兹曼公式实际上是对同一电离级的原子而言的。

一般实用的为对数形式：态和（配分函数）：

所以：任意能级上原子数目为：

萨哈公式

将分立能级的玻尔兹曼公式推广到连续态：其中：式子的右边仅仅是温度的函数，同样可以化为对数形式。

电离度

在这种原子的总数目中，次电离原子所占的比例：原子的电离级一般相距很远，往往只需要考虑两个相邻的电离级：

原子跃迁概率系数

自发发射概率系数：；受激发射/吸收概率系数：，所以单位时间在内发射光子的数目：吸收光子的数目：在热动平衡的条件下，，并代入玻尔兹曼公式：在时，应有，所以：再利用热动平衡下应等于普朗克函数: 原子的自发发射是各向同性的，而受激发射和吸收依赖于辐射场的方向，称受激发射为负吸收，则：与吸收的比值：最后一步用到玻尔兹曼公式

连续吸收的来源

光致电离

结合能为的原子可以吸收频率的任何光量子，从而产生一个连续吸收带，带头频率：并向短波方向延展。在考虑某一频率处的连续辐射的吸收，应考虑所有的吸收带作用的叠加

氢原子的连续吸收带：莱曼系限（ $Å$ ），巴耳末系限（ $Å$ ）...

自由—自由跃迁

自由电子在离子场中运动时，可以吸收光能量，也可以辐射光能量。

在自由态上原子的能量任意改变，所以可以吸收或辐射任何频率的光量子。

分子的吸收和散射

自由电子的汤姆孙散射和瑞利散射

外来电磁波作用于电子上时，电子会以同样的频率作强迫振动，向四面八方发出该频率的次波，这种现象为散射。

尘埃的散射和吸收

原子吸收系数 设原子的质量密度为，质量吸收系数为，质量为，单位体积内该原子的数目为，则：定义原子吸收系数：则：

类氢原子的吸收系数

光致电离的吸收系数

一个核电荷数的类氢原子，在主量子数为的能级上，原子吸收系数为(r代表r次电离)：其中为冈特因子。

由此可以看到，能级的吸收带从带头频率开始向高频端无限延伸，在带头频率处吸收系数最大，之后按衰减。带头处的吸收系数随n增大而增大。

在考虑恒星大气中的类氢原子的光电吸收时要注意：

研究某一频率的吸收，要考虑所有带头频率的吸收带
并非算数求和，而要考虑每个能级上的原子数目，加权叠加

自由—自由跃迁

以一个次电离原子计算的类氢原子自由-自由跃迁的吸收系数：

吸收系数的计算

以一个处于基态的类氢原子计算吸收系数，则有：式中的可以用玻尔兹曼公式得：

满足.

令代入里徳伯常量，可以得到常用的公式。类似可以引入以次电离原子（裸原子核）计算的吸收系数可以用玻尔兹曼公式和萨哈公式代入。

再加上自由-自由跃迁，设次电离原子的电离度为，则以该元素一个原子计算的吸收系数：推广到连续态，则需要考虑负吸收，最终的吸收系数：单位质量的吸收系数：