第一章：恒星大气辐射理论基础

恒星大气：最冷星3000K，最热星40,000K。恒星大气定义为恒星上产生可观测辐射的表面层。大气层下不透明的部分称为恒星内部。主要层次有：

1. 光球：白光观测到的表面层（黑体辐射，吸收线），薄
2. 色球：用单色光可看到的大气部分，产生发射线。用温度最小值处分为下色球层和上色球层。红色的辉光（线）
3. 冕：太阳大气最外层（韧致辐射），从射电直至x-射线波段都有辐射

描写辐射场的宏观物理量

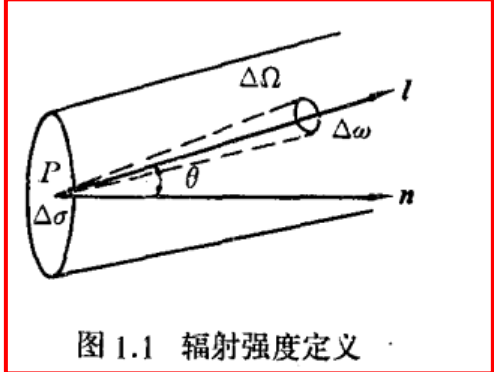
1. 辐射强度

2. 辐射流

   表示单位时间，单位频率间隔正向通过单位面积和反向通过的辐射能的差额，与面元在空间的位置和方向都有关系。

3. 平均辐射强度 即对对方向平均

4. 辐射密度 表示单位体积内包含的单位频率间隔的辐射能

5. 辐射压力 表示单色辐射施加于单位面积的压力

6. 总量：单色量对于所有频率的积分

辐射场微观描述

引入光子分布函数：表示在方向附近立体角内以光速传播的单位频率间隔的光子数，则： 由此可得到其他的宏观量。

发射系数、吸收系数和源函数

1. 发射系数

   设dm向各方向发射能量，则。所以有：

2. 吸收系数

   强度为的光束垂直投射到厚度为的无限薄表面上，光束强度减弱： 对此积分得： 指数定义为光学深度：

3. 源函数 发射系数和吸收系数之比

辐射转移方程

对于正入射情况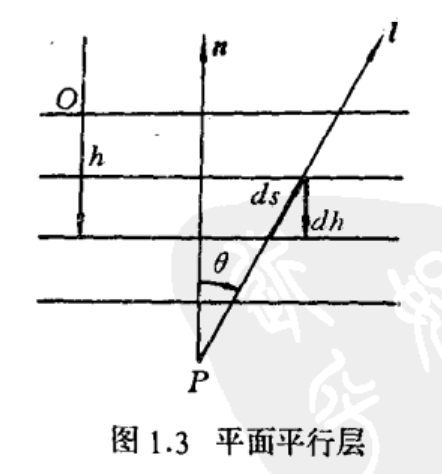： 对于恒星大气远小于恒星半径的情况，可以视为平面平行层，层法线与恒星半径同方向，则 辐射转移方程化为： 用光深作为自变量：

转移方程形式解

将向内和向外的辐射分开处理，向内辐射用作为参数。所以：

可得到形式解：

若要解出有用的解，还需要知道源函数和光学深度之间的关系

局部热动平衡假设

1. 理想热动平衡

1. 场内各点温度相同，且不变
2. 热辐射强度是均匀且各向同性，数值由普朗克函数确定
3. 满足基尔霍夫定理
4. 电子速度分布、原子的激发和电离可以分别用麦克斯韦分布、玻尔兹曼公式和萨哈公式描述

2. 局部热动平衡假设（LTE）

局部应用热动平衡关系，转移方程可化为：

辐射平衡

对于稳定的光球，每一体元的温度不随时间变化。 所以有： 如果在局部热动平衡的假设下： 由此还可以得出： 平面平行层大气的总辐射流是一个常数。 定义平均吸收系数以为权重，则： 则： 其中.所以总辐射压力对于光学厚度的微商也是常数。

灰大气近似

满足吸收系数与频率无关，即的物质称为灰色物质，由灰色物质组成的恒星大气称为灰大气。则辐射转移方程： 对于辐射平衡条件： 所以：

爱丁顿近似方法

引入三个量： 以乘转移方程，并对立体角积分： 由于为常数，所以： 爱丁顿引入第一近似： 代入： 利用边界条件：，所以，由此定出积分常数，得： 按照斯特凡-玻尔兹曼定律 即为温度分布的规律

太阳圆面临边昏暗规律

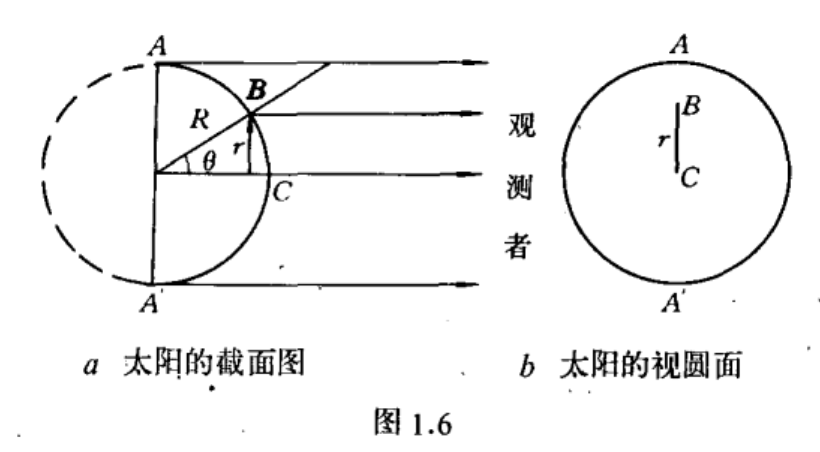1. 总辐射的临边昏暗规律 这里利用了爱丁顿近似下的温度分布并积分 2. 单色辐射的临边昏暗规律 采用波长标度，，易求出，代入辐射转移方程并引用温度分布规律 所以临边昏暗随着波长减小而越来越明显。